How and to what extent may quantum computing technology be used in the future?

Tom Brandis

IBM Q quantum computer

Abstract

Quantum computers are an exciting new type of computing that has many possible uses including cryptography, physical simulation and optimisation.

They can be used to create random numbers used in cryptography. Current methods will probably continue to be used in most situations as using quantum computers requires expensive hardware.

Secure quantum key distribution ensures that secret keys are not intercepted. It requires specialist hardware but is a useful technology that is likely to be used in high security environments in the future.

Quantum computers can theoretically break encryption when they get powerful enough, possibly in as soon as 20 years (2044). It is possible that encrypted information will be stored and decrypted in the future. Post-quantum cryptographic algorithms are being developed to counteract this.

Simulation of quantum materials on quantum computers could increase the accuracy of simulations and the range of scenarios that can be simulated however they need to get more powerful or improved algorithms be created before they are used practically. This could lead to development of new materials to solve problems.

An alternative form of quantum computing called quantum annealing is very good at solving optimisation problems. It has been already been used practically in a commercial situation.

Introduction

Quantum computers are a very different type of computer compared to those that surround us in everyday life. They use quantum phenomenon to create a new type of computing (Lu, n.d.). As well as bringing with them a new way to program, they have different advantages and problems to classical (non-quantum) computers. In this disseration I will examine how these advantages could be used in the future for cryptography, physical simulation and optimisation.

What is a quantum computer?

Whilst conventional computers are composed of bits, quantum computers use qubits.  A classical bit can be only a 1 or a 0, however,  a qubit can be anywhere in between (Wang, 2012). This is called superposition and a qubit is said to be in a superposition of 1 and 0. It also has a phase similar to that of a wave. This means that the qubit holds more information than a traditional bit.

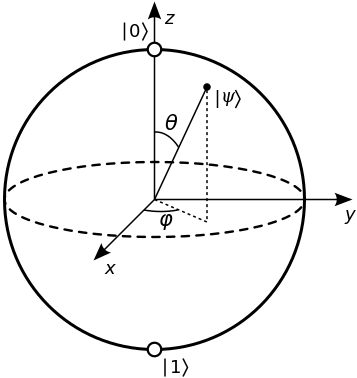
Bloch sphere (Glosser.ca, 2012) (available under CC BY-SA 3.0). A Bloch sphere can be used to represent all the possible states of a single qubit.

Not only can the qubits hold more information, they can also become 'entangled' with each other. This is when two different qubits become one quantum object through a quantum effect (Garisto, 2022). Changing one qubit then effects the other, allowing for increasingly complex operations as more qubits are added.

This can allow quantum computers to dramatically reduce the time taken for some types of calculations.

Cryptography

Cryptography is the process that allows for secure communication and is very important for ensuring privacy in an increasingly connected world.

In order to transmit information securely over the internet, data needs to be encrypted. This is the process of making information only readable if you have the digital key (Fortinet, 2024) and it prevents anyone else from being able to read private communications.

Successful encryption requires many parts, some of which quantum computers may be able to help with.

Random number generation

Randomness is extremely important for secure encryption as it is needed to make the secret key. If the key used for the encryption can be predicted by an interceptor of the message they will be able to read the information that you are trying to keep secret (Cloudflare, n.d.) (Baraniuk, 2024).

Quantum computers are an obvious choice for generating random numbers as they use the only truly random thing in the universe – quantum superposition. This is in contrast to conventional computers which are deterministic – meaning they always produce predictable results for a certain input.

Quantum computers can utilise superposition, a phenomenon where a qubit can be partially in multiple states. This allows us to create a qubit that is half 1 and half 0, using a gate called a hadamand gate.

When this qubit is read, and it's value is copied to a conventional bit, it will either be a 1 or a 0, but there is no way of knowing until it is done. This allows a quantum computer to use the true randomness in quantum mechanics to create the encryption key.

In order to see this in action, I used a IBM quantum computer that is available for students and researchers. It receives instructions using a programming library called Qiskit for the popular programming language python.

In the program below I create a circuit, which is a set of gates – basic quantum circuits that the computer applies to one or multiple qubits (Hou et al., 2014). This is composed of applying the hadamand gate individually to the qubits, putting them into a state of superposition between 0 and 1 and then reading them (Johnston et al., 2019), creating random numbers (IBM, n.d.). The random number is then printed.

1 # circuit produces a random number from 0 to 2^bits and works even when more bits are needed than quibits available

2 from qiskit import *

3 from qiskit.tools.visualization import *

4 from qiskit_ibm_runtime import QiskitRuntimeService

5 service = QiskitRuntimeService()

6 qcomputer = service.least_busy(simulator=False, operational=True)

7 simulator = Aer.get_backend('qasm_simulator')

8

9 backend = qcomputer

10 max_quibits = backend.num_qubits

11

12 def random_binary_circuit(length):

13 # create circuit

14 qr = QuantumRegister(length)

15 cr = ClassicalRegister(length)

16 circuit = QuantumCircuit(qr, cr)

17 circuit.h(qr)

18 circuit.measure(qr, cr)

19

20 # run circuit

21 result = execute(circuit, backend=backend, shots=1).result()

22 return list(result.get_counts(circuit).keys())[0]

23

24 def random_binary(length):

25 rand_bin = ""

26 full_circuits = length // max_quibits

27 partial_circuit_size = length % max_quibits

28 for _ in range(0, full_circuits):

29 rand_bin += random_binary_circuit(max_quibits)

30 if(partial_circuit_size):

31 rand_bin += random_binary_circuit(partial_circuit_size)

32

33 return rand_bin

34

35 if __name__ == "__main__":

36 random = random_binary(8)

37 print(random)

38 print(int(random, 2))

39

Python code using the qiskit library to set up and run the circuit that generates the random number on a quantum computer before outputting the results.

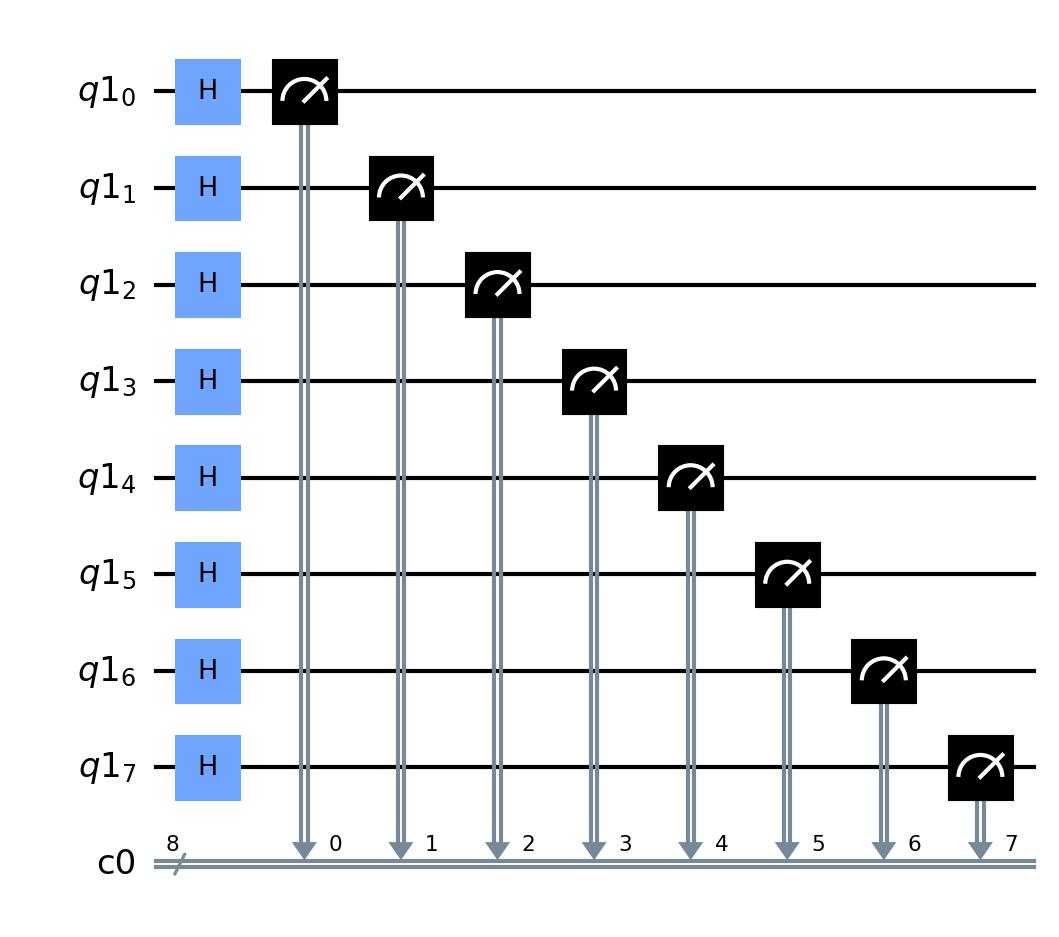
This is the circuit created by the code. Each qubit is put into a superposition using the hadamand gate (H) before being read/measured (gauge symbol).

I ran this on the quantum computer 'ibm_osaka' and it produced the random binary number 11001011 in 24.3 seconds.

In an encryption system, this random number could be used as a key to encrypt information.

One of the problems that holds this back from entering widespread use is the price of quantum computers. In order to be secure, the key has to be created locally, so that it isn't sent over the internet where it may be intercepted. This means that any organisations that want to use this would need to run their own quantum computer. This is a limitation for many organisations as quantum computers are very expensive to buy – a commercial 9-qubit computer is available for $900,000 (~£700,000) (The Quantum Mechanic, 2024). although a (less useful) 2-qubit computer is available for just $5,000 (~£3,900) (The Byte, 2021).

A quantum computer designed for true random number generation is for sale by a QuintessenceLabs (2024), indicating that there is a market for this, however the price is only on request (Sharma, 2017). It may be prohibitively expensive compared to other, non‑quantum solutions.

Whilst using a quantum computer is possibly the only way of creating a completely random number, methods have been designed for very hard to predict numbers called pseudo-random numbers using a classical computer system. A hard to predict number is taken from the outside world, this is called a seed (Cloudflare, 2013). This is a number that an attacker cannot guess easily such as the last few digits from a temperature sensor. This is called statistically random noise and whilst it is not technically completely random, it is widely considered to be unpredictable enough for most situations. Sources of statistically random noise have a level of entropy or 'randomness' and combining multiple sources always increases this. For this reason, seeds are often composed of multiple sources of statistically random noise combined.

This seed is then put through a pseudo-random number generator that produces a very different number even for very similar seeds. If the seed is not random enough it can lead to encryption being broken—for example if time is used it can easily be predicted. This makes it a bad source for a seed.

As there is already an accepted solution to this problem, quantum computers are unlikely to be used for it except in situations where security is extremely important, until quantum computers become significantly cheaper.

Secure message transmission

After a key is generated, it can be used in encryption.

Typically asymmetric encryption is used for communication, with a private and public key – a non-secret public key is given to the sender by the receiver. This is used to encrypt the information so that only the receiver can decrypt it. This is analogous to a locked post box – anyone can put information in but only the person with the private key can read it.

However due to the fact that there is a mathematical relationship between the public and private keys, it is possible to calculate what the private key is in some situations, although it generally is not feasible without a lot of time and computing power.

If an attacker cannot access even the public key, there is no way for them to find the private key and read the message. If the key could be sent securely to the sender, then the system could be completely secure. This is desirable to many organisations that handle valuable or confidential information.

One potential way to do this is quantum key distribution.

In quantum key distribution, information is sent as qubits in superposition. A practical way to do this could be a dedicated fibre optic cable, along which individual photons are sent. The photons would act as the qubits, and could be put into a superposition of states, with the key value stored in how much they are 0 or 1.

The main advantage of this system is that if read, the photons state will collapse into either 1 or 0, rather than a superposition (Giles, 2019). Due to the uncertainty principle, all the information cannot be learned about a qubit simultaneously. This means that the interceptor cannot ever learn enough of the information in the qubit to produce a copy to transmit to the receiver (Ghose, 2018), meaning the receiver will be able to tell if the qubit was intercepted.

If the receiver detects that a key is intercepted in transmission, they can request a new one. This means that when they decide to use a key to transmit the message they can be sure that the key is not known by anyone else and that the message is secure.

The main barrier to deployment of this technology in areas like government agencies is that in order to preserve the quantum information on the photons, 'repeaters' or 'relays' which allow to photon to travel longer distances need to be designed in order to not collapse the superposition (van Loock et al., 2020).

Breaking encryption

Asymmetric encryption being secure is very important as many important services such as online shopping and private communication rely on it. If an attacker could intercept and decrypt a shopping transaction they may be able to compromise a users bank account and steal their money. Likewise private or personal information could be stolen from a private message.  

In asymmetric encryption, a public key is created by multiplying together large prime numbers from the secret key. This is considered secure as it would take a computer a very long time to factorise the public key into the secret key – possibly longer than the age of the universe for a longer key.

Quantum computers could potentially be much quicker at doing this than classical computing methods. Shor proposed a way to do this called Shor's algorithm (1994).  

However there is a problem with this—whilst Shor's algorithm theoretically works, quantum computers rely on very precise measurements of qubits, which are usually either very small superconducting circuits (Kjaergaard et al., 2020) or trapped ions (IonQ, 2024) When they have thermal energy – heat – it causes them to vibrate, introducing error into the measurements. To minimise this, qubits are cooled to as close to 0K (‑273.15°C) as possible however, the heat cannot be completely removed. Hardware is also not completely precise. Photons of light are another alternative (Xanadu, 2024) however they have the disadvantage of having limited interactions between each other and are easily absorbed (Bassman et al., 2021). This means current quantum computers are too error prone to be able to factorise big numbers such as those used in encryption.

To further reduce error resulting from qubit vibration, the results from multiple physical qubits are combined programmatically into a single logical qubit to mitigate the error. This logical qubit is used in computations (Shaw et al., 2008).

The largest number factorised by a quantum computer using Shor's algorithm (without prior knowledge of the answer) is 15 (Monz et al., 2016). It used only 7 qubits, meaning that it would have taken $2^7$  (128) operations on a classical computer, a very small amount, however other methods have been used to factorise up to 376,289 (Jiang et al., 2018). These numbers are much shorter at 4 bits and 19 bits respectively than the typical 2,048 bit length of keys used on the internet. Other, larger factorisations have been claimed, however they rely on knowing the answer before and changing the algorithm.

In this respect, quantum computers are not yet useful for breaking encryption.

Whilst quantum computers cannot yet outperform classical computers in breaking encryption, it seems to be likely that they will be able to in the near future. Some predict current algorithms will be breakable by quantum computers as soon as 2044 (Computer Security Division, 2024), although I think that it will likely be longer.

There is also a fear that data that is currently secured using vulnerable algorithms might be stolen and kept until quantum computers become good enough to break it (O’Neill, 2021).

As new cryptography algorithms can take a long time to be deployed, 'post‑quantum' algorithms that are resistant to being broken by a quantum computer are now being created.

Simulating quantum systems

Quantum materials are materials with properties that can “only be described by the laws of quantum mechanics” (Bassman et al., 2021). These are usually materials that work on a very small scale. Some have unique properties such as being superconductors, topological insulators or multiferroics (Oxford Department of Physics, 2024). They have the potential to be useful in many fields such as sensing, communication, metrology, energy storage and pharmaceutical development (Broholm et al., 2016), making them important for the future.

This is because they could be used to simulate objects that have to be accurate down to a very small scale such as proteins or novel batteries to a much higher degree of accuracy than a conventional computer.

This makes simulation on quantum computers a useful tool when developing new quantum materials, as it means that materials properties can be estimated before it is created. As new materials can be expensive and physically complicated to create, being able to assess if a material may be useful before making it is very useful.

This also means that researchers can look for materials with specific properties by testing many simulated materials for desired properties, allowing solutions to specific problems to be found.

Additionally, physicists frequently use computer simulations in order to test hypotheses. For example a simulation of gas and dust forming into planets allowed scientists to determine that young planets are likely to be oblate spheroids rather than perfect spheres (BBC, 2024). This created a better understanding of young planets and informs astronomers that the planets are likely to look different when viewed at different angles.

Another example of a computer simulation being used is a simulation of what the new James Web Space Telescope's (JWST) Near-Infrared camera would see in various situations. This allowed scientists to interpret the images that the camera itself produced (Burke et al., 2019).

In some cases, such as the strong nuclear force, calculations are too hard for classical computers (Brooks, 2023). This force determines how quarks bind together to make protons and neutrons and how they then form particles. Being able to simulate this could lead to a better understanding of how particles work.

Simulation has been historically performed on classical computers, however, when simulating a quantum system, complexity—and the processing power needed—rises exponentially with the system size. This means that systems with more than a few atoms need huge amounts of processing power. This complexity is usually reduced to polynomial (scaling in line with the size of the system) using density functional theory (Harrison, 2001) however this comes at the cost of accuracy and doesn't work when the parts of a system are highly quantum entangled (Bassman et al., 2021, p. 3).

To perform more accurate simulations or simulations on entangled quantum systems, a quantum computer can be used. When a quantum computer is used to simulate the system it allows for polynomial scaling of complexity without making approximations.

This is because qubits can be used to store the state of a quantum particle and the evolution of the system can be efficiently simulated (Bassman et al., 2021, p. 4). The components of the system are represented as wave functions rather than as objects with conventional position and momenta.

Last year, a particle was simulated on a quantum computer (Motta et al., 2023). The successful simulation used IBM’s Falcon processor which has just 27 qubits, many less than the biggest quantum computers (Brooks, 2023).

Although this seems to be one of the best uses of quantum computers, limitations of current quantum computers mean that this hasn't yet been used in practical situations. However, Bassman (2021, p. 4) believes that better algorithms could make simulating on quantum computers possible for real materials without improvements to the hardware itself.

Optimisation problems

Optimisation is “the process of making something as good or effective as possible” (Cambridge University Press, 2024) or “search[ing] for the best of many possible combinations” (D-Wave Systems, n.d.). This involves changing variables in a situation, usually to create the best outcome, making it important to many businesses.

To optimise a situation, we first need to find a number to represent how good the situation is in different solutions, based on variables we can change, so that they can be compared and we can find the best one.

This number is the solution to a cost function. Singh defines this as a “function that plots an event or values of one or more variables in a real number” (2016). A linear cost function is given as:

$$C(x)=\mathit{FC}+V(x)$$

where C(x) is the cost for x units, FC is the fixed costs and V is the cost per item. (DataScience, n.d.)

A simple, linear example of a cost function could be a shop. If the shop pays £500 per year in rent (and other fixed costs) and each item they sell costs them £10 to buy then this would be the cost function:

$$C(x)=500+10(x)$$

from this we can figure out the cost to the business depending on how much they sell.

Cost functions can be used for more complicated situations, leading to functions with high powers.

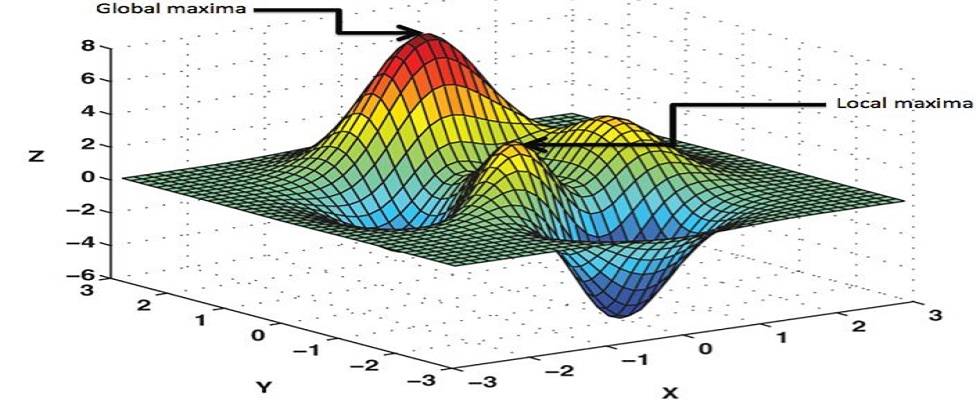Visualisation of a complicated cost function (Filippo Venezia, n.d.)

Once the cost function has been determined, the maximum or minimum point has to be found in order to find the best solution to the problem. This can be done with a classical computer however it can become very time consuming with many variables.

Quantum annealing

As cost functions become more complicated, they take more time to solve. A special type of quantum computer called a quantum annealer can be used to solve these complex functions in a smaller amount of time.

This works because cost functions are similar to an energy minimisation problem. Qubits can be used with a process that increases and decreases a variable called “heat” that defines how likely they are to go to a higher energy level until a global energy minimum is found. This allows a minimum from a larger area to be found, as the energy can increase (over a local peak) before finding the lowest point (D-Wave Systems, n.d.). This can be used to solve cost functions.

This quantum annealing has been used to solve many problems already such as logistics optimisation at the Port of LA, driver scheduling optimisation for a food provider company (D-Wave Systems, 2024) and by plane manufacturer Airbus to calculate the best trajectories for flights (Ardelean, n.d.).

Despite this commercial use, there are not many companies that provide it as a service, which is the most practical way that companies could access optimisation with quantum annealing. I found just 2, Quantagonia (n.d.) and D-Wave Systems (2023). Airbus seem to have run the optimisation themselves, however this is only really possible for very large companies. This situation may be because quantum annealing is only advantageous for very complicated optimisation problems, so the market is quite small. As the technology become more accepted, more companies may start providing optimisation using quantum annealing.

Conclusion

In conclusion, quantum computers are a new type of computer that uses qubits instead of bits to both store more information per bit using superposition of state and phase as well as allowing them to interact with each other via entanglement.

They seem likely to change the field of cryptography. Superposition can be used to create random numbers although this currently requires expensive hardware meaning that current methods will probably continue to be used in most situations.

Distribution of keys using photon qubits could allow cryptographic keys to be shared more securely as the uncertainty principle means that any interception could be detected. This requires expensive specialist fibre optic cable infrastructure so will probably only be used in the most secure situations.

Quantum computers cannot yet break encryption in a meaningful way, although the biggest may be able to within the next 20 years. This has lead to fears that encrypted information will be recorded now and decrypted later when the encryption can be broken. Cryptographic algorithms that are resistant to being broken by quantum computers are now being created in order to prevent this.

Accurate simulation of materials taking quantum effects into account may be able to be competed more efficiently on quantum computers than using conventional methods. This could lead to discovery of new quantum materials and materials to solve specific problems. Current quantum computers are not powerful enough to simulate large enough systems to be useful however they are likely to get better over time.

Solving optimisation problems are useful in many situations and quantum computers may be able to allow very complex problems to be solved. This can lead to better efficiency and less wastage as more variables can be taken into account. Quantum optimisation is already being done using a type of quantum computer called a quantum annealer.

Whilst it is hard to predict how quickly the field will advance in the future, as quantum computers improve, these uses are likely to become more viable and enter more widespread usage.

Self evaluation

Why did I choose this topic?

Before I started this EPQ, quantum computing was something that I had heard about but didn't really understand. When I was deciding on an EPQ, I wanted to learn something new and interesting to me rather than spending time on something I already knew about.

The topic of quantum computers additionally contains elements of both computer science and physics. These are interests of mine that I have taken at A level and I knew that I wanted to take one of them further to university. Doing this EPQ helped me to decide to study physics at university. It gave me an insight into how broad the subject is outside of the A level and GCSE specifications.

Limitations

Whilst I used many sources, I could not read all the published material on the topic. I also relied on specialised search engines such as Google Scholar, CORE and RefSeek as well as general purpose search engines to find possible uses for quantum computers, meaning that I may have missed a less well known possible uses. I also could not access papers published by a few journals as they required a subscription, which may have lead to me missing information.

I also did not research every possible use but instead focused on a few main areas that I was particularly interested in.

What have I learned?

Doing this EPQ was the first time that I worked on a written project of this scope. It helped me to improve my report writing skills. Additionally I improved my time management over the course of the project. It also helped me improve my researching. As part of the project I learned to use the qiskit python library to write code that runs on quantum computers. It is not widely known that IBM make a quantum computer available to students and researchers, therefore I was pleased to find out that I was able to access this computer and was able to write code to run on it.

I also enjoyed presenting as it allowed me to explain verbally what I learned.

Bibliography